вопрос
Вопрос в том: как поставить сортировку новостей и комментариев по алгоритму в DLE?
Стандартно стоит на DLE 5 звезд, и если например поставить + и - то алгоритм соответственно надо менять.
Почему это правильно. Нам необходимо найти баланс между долей положительных оценок и неопределенностью малого числа наблюдений. К счатью, математический аппарат для решения этой проблемы был разработан в 1927 году Эдвином Вильсоном. Мы хотим знать следующее: «Обладая набором данных мне оценок, можно ли с вероятностью 95% сказать, какова будет „реальная“ доля положительных оценок?». Вильсон дает ответ. Учитывая только положительные и отрицательные оценки (т.е. не беря во внимание 5-бальную систему оценивания), нижняя граница доли положительных оценок вычисляется по следующей формуле:
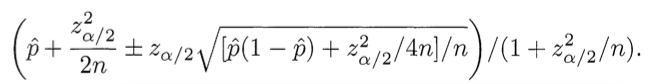
Используйте минус там, где написано плюс/минус, чтобы вычислить нижнюю границу. Здесь p̂ — доля положительных оценок, zα/2 есть квантиль* (1-α/2) стандартного нормального распределения, и n есть общее число оценок. Аналогичнная формула, примененная на Ruby:
*Кванти́ль в математической статистике — значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Wikipedia
Тут pos — число положитеьных оценок, n — общее число оценок, а confidence задаёт статистически доверительный уровень: установите его в 0.95, чтобы с 95% вероятностью рассчитывать на правильность нижней границы, в 0.975, чтобы иметь 97.5% вероятности. Число z в этой функции никогда не меняется. Если у вас нет удобного программного обеспечения для работы со статистическими данными или же для вас критична производительность, вы можете всегда жестко прописать значение для z. (Используйте 1.96 для доверительного уровня в 0.95).
Ниже в качестве иллюстрации приведём SQL запрос, делающий что нам нужно. Предполагаем, что у нас есть таблица объектов с положительными и отрицательными оценками по ним, и мы хотим отсортировать их по нижней границе 95% доверительного интервала:
Думаю это очень важный вопрос! Давайте разберемся =)

Вопрос в том: как поставить сортировку новостей и комментариев по алгоритму в DLE?
Стандартно стоит на DLE 5 звезд, и если например поставить + и - то алгоритм соответственно надо менять.
Рейтинг = Нижняя граница доверительного интервала Вильсона (Wilson) для параметра Бернулли
Почему это правильно. Нам необходимо найти баланс между долей положительных оценок и неопределенностью малого числа наблюдений. К счатью, математический аппарат для решения этой проблемы был разработан в 1927 году Эдвином Вильсоном. Мы хотим знать следующее: «Обладая набором данных мне оценок, можно ли с вероятностью 95% сказать, какова будет „реальная“ доля положительных оценок?». Вильсон дает ответ. Учитывая только положительные и отрицательные оценки (т.е. не беря во внимание 5-бальную систему оценивания), нижняя граница доли положительных оценок вычисляется по следующей формуле:
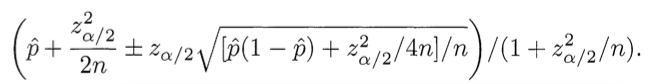
Используйте минус там, где написано плюс/минус, чтобы вычислить нижнюю границу. Здесь p̂ — доля положительных оценок, zα/2 есть квантиль* (1-α/2) стандартного нормального распределения, и n есть общее число оценок. Аналогичнная формула, примененная на Ruby:
*Кванти́ль в математической статистике — значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Wikipedia
require 'statistics2'
def ci_lower_bound(pos, n, confidence)
if n == 0
return 0
end
z = Statistics2.pnormaldist(1-(1-confidence)/2)
phat = 1.0*pos/n
(phat + z*z/(2*n) - z * Math.sqrt((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n)
end
Тут pos — число положитеьных оценок, n — общее число оценок, а confidence задаёт статистически доверительный уровень: установите его в 0.95, чтобы с 95% вероятностью рассчитывать на правильность нижней границы, в 0.975, чтобы иметь 97.5% вероятности. Число z в этой функции никогда не меняется. Если у вас нет удобного программного обеспечения для работы со статистическими данными или же для вас критична производительность, вы можете всегда жестко прописать значение для z. (Используйте 1.96 для доверительного уровня в 0.95).
Ниже в качестве иллюстрации приведём SQL запрос, делающий что нам нужно. Предполагаем, что у нас есть таблица объектов с положительными и отрицательными оценками по ним, и мы хотим отсортировать их по нижней границе 95% доверительного интервала:
SELECT
widget_id,
((positive + 1.9208) / (positive + negative) -
1.96 * SQRT((positive * negative) / (positive + negative) + 0.9604) /
(positive + negative)) / (1 + 3.8416 / (positive + negative))
AS ci_lower_bound
FROM widgets WHERE positive + negative > 0
ORDER BY ci_lower_bound DESC;
Думаю это очень важный вопрос! Давайте разберемся =)



